Mod Set Theory When we add or subtract multiples of n from an integer x to reach some y in mathbb Z n we say are reducing x modulo n and y is the residue We could have
Modular arithmetic is a system of arithmetic for integers which considers the remainder In modular arithmetic numbers wrap around upon reaching a given fixed quantity this given quantity is known as the modulus to leave a remainder A number a has an inverse modulo 26 if there is a b such that a b 1 mod 26 or a b 26 k 1 thus we are looking for numbers whose products are 1 more than a multiple of 26
Mod Set Theory

Mod Set Theory
https://lookaside.fbsbx.com/lookaside/crawler/threads/C9rwjVFMN0l/0/image.jpg

FANTASTICA JASMINE PAOLINI Conquista Gli Ottavi Di Finale Alle
https://lookaside.fbsbx.com/lookaside/crawler/threads/C-AU7s3tvjT/0/image.jpg

Maison bedding set white 03 03 jpg
https://shezhomemall.openhost.cafe24.com/product/bedding/maison/new/maison_bedding_set_white_03_03.jpg
Problem 2009 PUMaC Number Theory Problem A1 If 17 355687ab8096000 where a and b are two missing digits nd a and b Problem 2004 AIME II Problem 10 Let S Definition Modulo Let m in mathbb Z a is congruent to b modulo m denoted as a equiv b mod n if a and b have the remainder when they are divided by n
Modular arithmetic is a generalization of parity We say a b mod n if n divides a b There are n residue classes modulo n That is every integer is congruent to one of 0 1 2 3 n 1 In the Chapter on Set Theory we discussed the idea of relations 1 and specifically provided the example of modular equivalence on this page In there we stated that the relation
More picture related to Mod Set Theory

Maison bedding set beige 03 01 jpg
https://shezhomemall.openhost.cafe24.com/product/bedding/maison/new/maison_bedding_set_beige_03_01.jpg
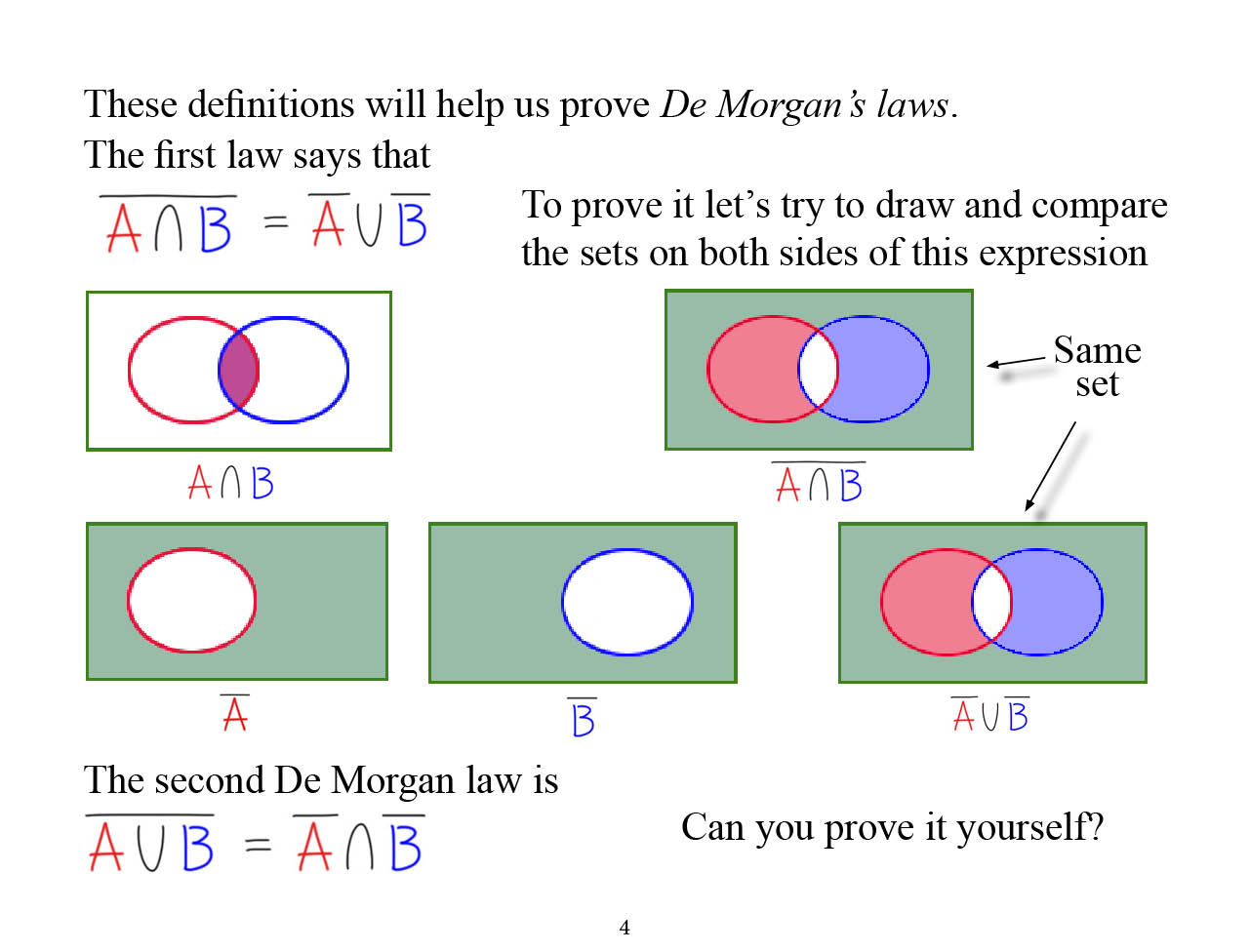
TinyTram Math Set Theory
http://tinytram.com/wp-content/gallery/math_sets_en/sets_en05.jpg

Power Rangers Dino Charge Pics Infoupdate
https://i.ebayimg.com/images/g/aW0AAOSwvWBjga1m/s-l1600.jpg
Classes modulo n A set containing exactly one integer from each congruence class is called a complete system of residues modulo n Examples The set 0 1 2 n 1 of remainders is a Set theory is a branch of mathematical logic that studies sets which are collections of objects These objects are called elements of the set Learn complete set theory
Set theory studies sets the fundamental building blocks of mathematics While logic describes the language of all mathematics set theory provides the framework for additional structures In Every set class has a complementary set class i e pentachord heptichord tetrachord octachord and trichord nonachord All sets can be placed into set class families

Nude Photo Set Of Chinese Model Mao Mao 35 481
https://img.xchina.biz/photos/655ef79507797/0035.jpg

Cute Aesthetic Pictures For Stickers Infoupdate
https://png.pngtree.com/png-clipart/20221224/original/pngtree-cute-aesthetic-journal-sticker-set-png-image_8801448.png

https://crypto.stanford.edu › pbc › notes › numbertheory › arith.html
When we add or subtract multiples of n from an integer x to reach some y in mathbb Z n we say are reducing x modulo n and y is the residue We could have

https://brilliant.org › wiki › modular-arithmetic
Modular arithmetic is a system of arithmetic for integers which considers the remainder In modular arithmetic numbers wrap around upon reaching a given fixed quantity this given quantity is known as the modulus to leave a remainder

Nude Photo Set Of Chinese Model Quiet Hotel 501 501

Nude Photo Set Of Chinese Model Mao Mao 35 481

Nude Photo Set Of Chinese Model Xiaolan 2 82

Nude Photo Set Of Chinese Model Xiao Meng 3 288

Products Eden Promosyon

Nude Photo Set Of Chinese Model Xiaolan 11 82

Nude Photo Set Of Chinese Model Xiaolan 11 82

Nude Photo Set Of Chinese Model Ji eun 1 1200

Nude Photo Set Of Hongkong Model Pinky 5 210

Nude Photo Set Of Chinese Model Yu Zihan 4 519
Mod Set Theory - Modular arithmetic is a generalization of parity We say a b mod n if n divides a b There are n residue classes modulo n That is every integer is congruent to one of 0 1 2 3 n 1