Antiderivative Of 1 Sin2x The antiderivative of a constant follows the same rules as the antiderivative of a power function Just picture the constant with a variable x raised to the power of 0 Any
Think of a simpler example if all we have available as elementary functions are polynomials or more generally rational functions the function 1 x wouldn t admit an elementary This means that int x x dx has no elementary antiderivative The specific reason to take mathbb Q x log x g as our differential field is that it is a field of trascendental
Antiderivative Of 1 Sin2x
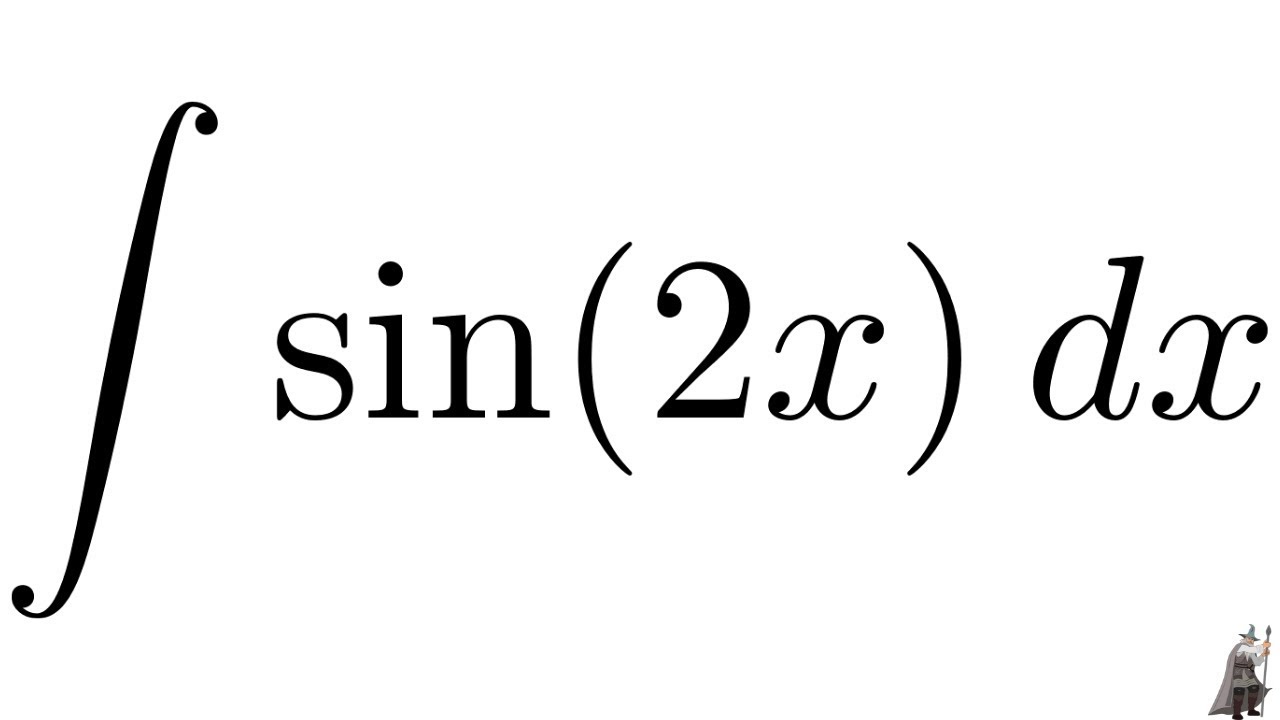
Antiderivative Of 1 Sin2x
https://i.ytimg.com/vi/xN2k89EhM1E/maxresdefault.jpg

How To Integrate Sin 2x cos 2x YouTube
https://i.ytimg.com/vi/P3_F8agLeXU/maxresdefault.jpg
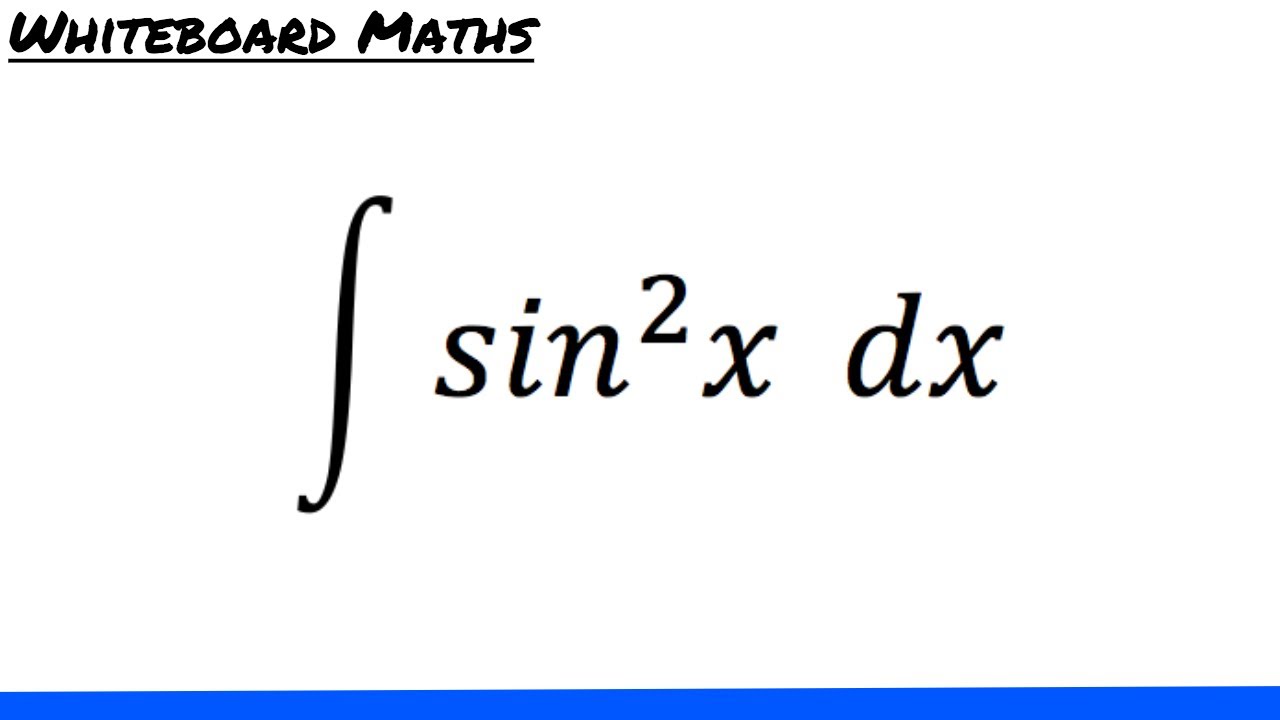
Integral Of Sin 2 X YouTube
https://i.ytimg.com/vi/9BHC0VLf5-4/maxresdefault.jpg
Using indefinite integral to mean antiderivative which is unfortunately common obscures the fact that integration and anti differentiation really are different things in general Stack Exchange Network Stack Exchange network consists of 183 Q A communities including Stack Overflow the largest most trusted online community for developers to learn share their
This is a contradiction and there is no antiderivative Edit I see you have edited your question so I will edit my answer Your second equation about winding numbers is true because of the The antiderivative of frac 1x is the function whose inverse is exactly equal to its own derivative
More picture related to Antiderivative Of 1 Sin2x

Q11 Evaluate The Definite Integral From 0 To 4 1 sin2x Limit 0
https://i.ytimg.com/vi/iRdiOJOmdKo/maxresdefault.jpg

How To Integrate Xsin 2x Integration By Parts Worked Example YouTube
https://i.ytimg.com/vi/QVyARWESeSw/maxresdefault.jpg
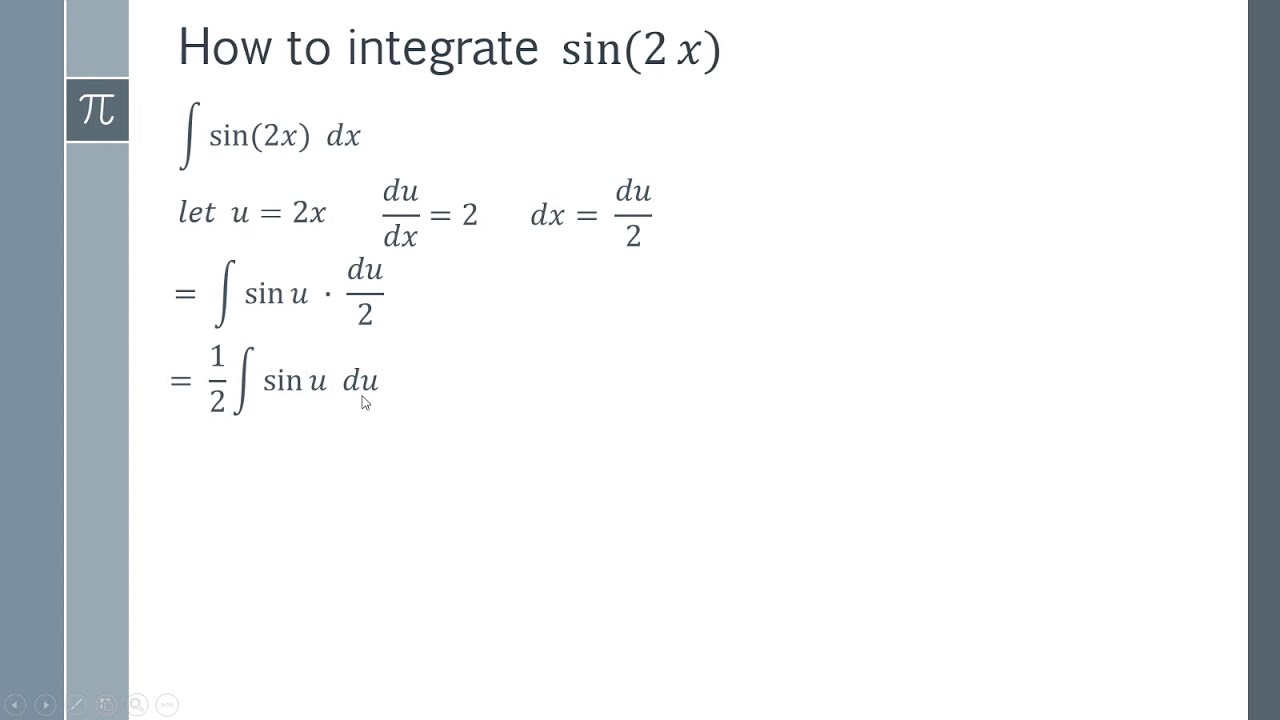
How To Integrate Sin 2x Step By Step Integration Proof YouTube
https://i.ytimg.com/vi/M0sZoPvf9Aw/maxresdefault.jpg
One is the question of why the definite Riemann integral gives the correct notion of area under a curve for a nonnegative Riemann integrable function The other which As we know a non continuous function may have an antiderivative Thus the function may not be integrable That is although there is an explicitly defined antiderivative F x possibly not but
[desc-10] [desc-11]

Integral Of 1 1 sin 2x trigonometric Identities Substitution
https://i.ytimg.com/vi/YyRRStiPWwU/maxresdefault.jpg

NO OF SOLUTION OF 1 sin2x 4 3cosx sin2x YouTube
https://i.ytimg.com/vi/YNpE5ffyvhs/maxresdefault.jpg?sqp=-oaymwEmCIAKENAF8quKqQMa8AEB-AH-CYAClgWKAgwIABABGFsgZShfMA8=&rs=AOn4CLBn5cS9MgFdQ1N8VjLi4QgJUiXifA

https://study.com › academy › lesson › antiderivatives-of-constants-pow…
The antiderivative of a constant follows the same rules as the antiderivative of a power function Just picture the constant with a variable x raised to the power of 0 Any

https://math.stackexchange.com › questions
Think of a simpler example if all we have available as elementary functions are polynomials or more generally rational functions the function 1 x wouldn t admit an elementary

Integral Of sin 2x cos 2x Calculus 1 Trig Integrals YouTube

Integral Of 1 1 sin 2x trigonometric Identities Substitution
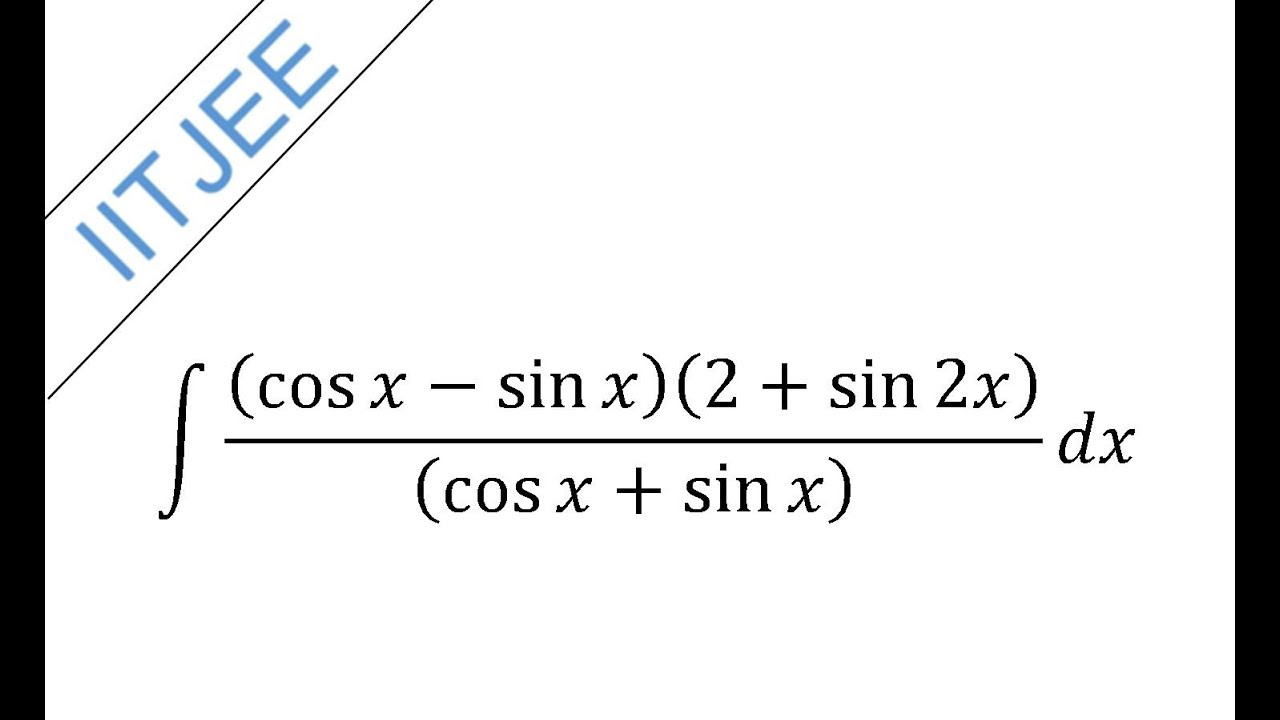
Integrate cosx sinx 2 sin 2x cosx sinx Indefinite Integral 7

Integration Of Root Of 1 Sin2x IITJEE 2024 JEE MAINS 2024

Integral Sin 2 x cos x Integration Of Sin 2 x cos x

Integral Of 1 1 sin 2 x T Tan x Substitution For Integrating

Integral Of 1 1 sin 2 x T Tan x Substitution For Integrating

Integration 0 To Pi 4 Root Over Of 1 sin2x Dx Solution KVS PGT

Integral Of 1 sin2x 0 5 Integral Of Square Root 1 sin2x Sqrt 1
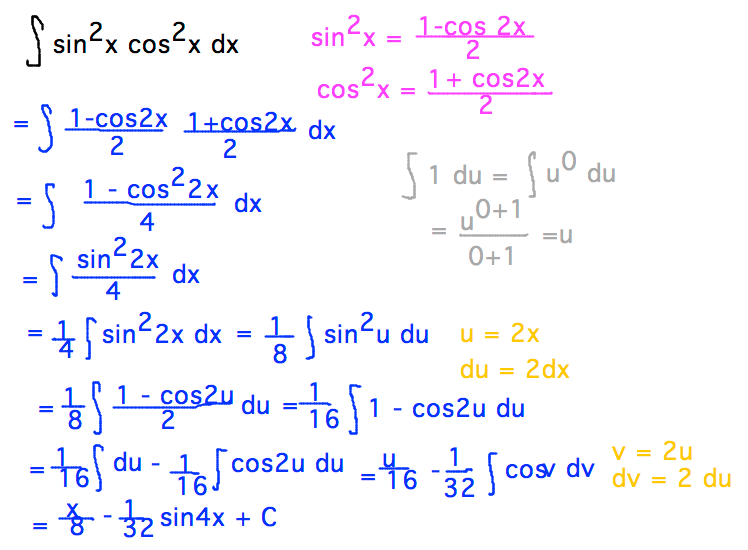
Geneseo Math 222 01 Integration
Antiderivative Of 1 Sin2x - This is a contradiction and there is no antiderivative Edit I see you have edited your question so I will edit my answer Your second equation about winding numbers is true because of the