Orthogonal Rotation In Exploratory Factor Analysis Results In I have often come across the concept of orthogonality and orthogonal functions e g in fourier series the basis functions are cos and sine and they are orthogonal For vectors
An orthogonal basis can be used to decompose something into independent components For example the Fourier transform decomposes a time domain function into Two vectors are orthogonal if their inner product is zero In other words langle u v rangle 0 They are orthonormal if they are orthogonal and additionally each vector has
Orthogonal Rotation In Exploratory Factor Analysis Results In

Orthogonal Rotation In Exploratory Factor Analysis Results In
https://i.ytimg.com/vi/BlFtfZXNl8Q/maxresdefault.jpg

What Is Exploratory Research When We Do This Steps Of Exploratory
https://i.ytimg.com/vi/5ZnzmJQ0aNI/maxresdefault.jpg

Exploratory Factor Analysis Step 3 5 Total Variance Explained
https://i.ytimg.com/vi/eh6fduxszQ8/maxresdefault.jpg
To expound upon the definition of orthogonal spaces you can prove that planes are orthogonal by using their basis elements Each 2d plane has two basis elements and everything in the Generally those matrices that are both orthogonal and have determinant 1 are referred to as special orthogonal matrices or rotation matrices If I read orthonormal matrix somewhere I
Now find an orthonormal basis for each eigenspace since the eigenspaces are mutually orthogonal these vectors together give an orthonormal subset of mathbb R n Finally Rahul That s the whole point of the orthogonalization In the raw coding you can only interpret the p value of speed of speed 2 remains in the model And as both regressors
More picture related to Orthogonal Rotation In Exploratory Factor Analysis Results In

Parallel Analysis
https://pic4.zhimg.com/v2-f34674d6b3805a0623f7e7c9d4e13533_r.jpg

Final Exam Factor Analysis Diagram Quizlet
https://o.quizlet.com/mc3rbLGImWj8SEuHs07-LA_b.png

Exploratory Factor Analysis conceptual YouTube
https://i.ytimg.com/vi/Q2JBLuQDUvI/maxresdefault.jpg
begingroup Freeze S If you re only talking about matrices then orthogonal maps coordinate lines in one orthogonal frame to orthogonal lines in another Unitary does the same Matrices represents linear transformation when a basis is given Orthogonal matrices represent transformations that preserves length of vectors and all angles between
[desc-10] [desc-11]
GitHub GYKrishna25 EDA with Python Projects
https://repository-images.githubusercontent.com/564395828/542d79b6-e8d8-4c73-8a5f-d186397dc0cc
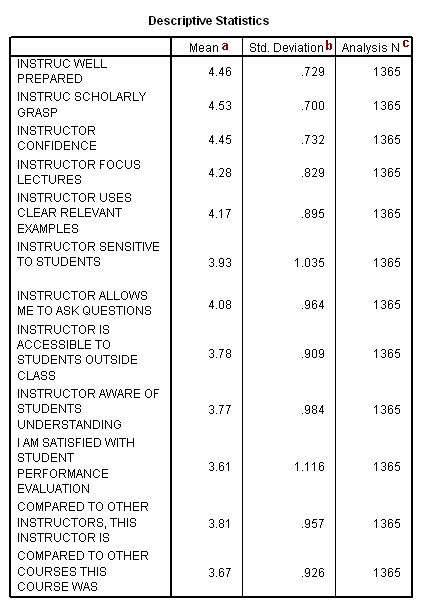
Principal Components Analysis SPSS Annotated Output
https://stats.idre.ucla.edu/wp-content/uploads/2016/03/spss_output_f1_0.png

https://math.stackexchange.com › questions
I have often come across the concept of orthogonality and orthogonal functions e g in fourier series the basis functions are cos and sine and they are orthogonal For vectors

https://math.stackexchange.com › ... › difference-between-perpendicula…
An orthogonal basis can be used to decompose something into independent components For example the Fourier transform decomposes a time domain function into

Factor Analysis
GitHub GYKrishna25 EDA with Python Projects

Factor Analysis
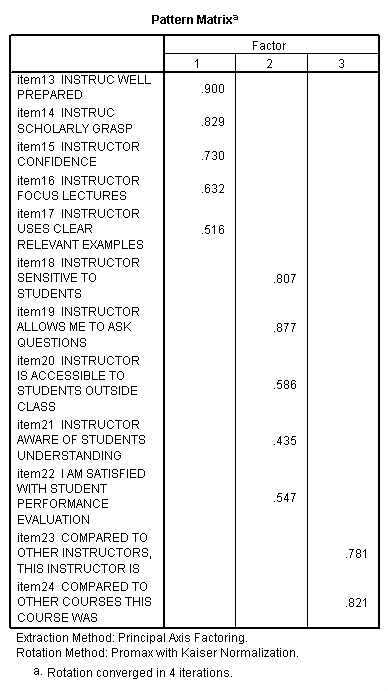
Factor Analysis SPSS Annotated Output

Exploratory Factor Analysis Results Download Scientific Diagram

Cross Loading Discriminant Validity Download Scientific Diagram

Cross Loading Discriminant Validity Download Scientific Diagram

Orthogonal Matrix
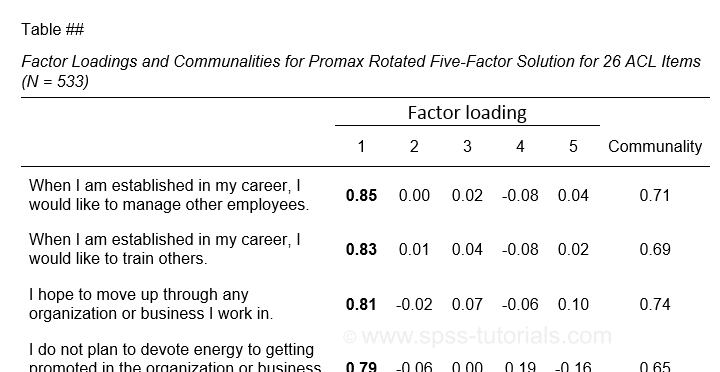
APA Style Reporting Factor Analysis

Factor Analysis Steps Methods And Examples Research Method
Orthogonal Rotation In Exploratory Factor Analysis Results In - Rahul That s the whole point of the orthogonalization In the raw coding you can only interpret the p value of speed of speed 2 remains in the model And as both regressors